Chockstone Forum

      Sponsored By
      ROCK
   HARDWARE

Chockstone Photography

Australian Landscape Prints

Chockstone Forum - Gear Lust / Lost & Found

Rave About Your Rack Please do not post retail SPAM.

Author

Impact factor calculations and microwire placement


ajfclark

24-Nov-2009
12:17:28 PM

On 24/11/2009 egosan wrote:
>Why stop there, Neil?

Neil hasn't said anything... So shouldn't he be starting?


Chuck Norris

24-Nov-2009
10:30:56 PM

I belayed a guy who blew two 0 rps (both in same placement). They held quite a few 6ft falls before busting and broke mainly cos of wire wearing over rock.

I've taken a few decent lobs on #1 rps. When they are bomber placements you'd be surprised how much they will hold - trouble is most of the time when the placement is that small you only need a slight blemish in the placement to turn it into a piece of shit.

Finally, regarding the situation mikl mentioned - surely having gear rip all the way to a grounder is preferable to a free fall to the deck?

mikl law

26-Nov-2009
8:08:48 AM

It's got to help, but
a) it's better to have a strategy (equalising, double ropes, slipepry belay) which makes it stay in.
b) the amount of energy absorbed (= speed reduction) is small if the gear fails.

A few assumptions follow here, particularly that ropes have a linear force stretch, that air rsistance is ignored, and I've ignored the extra energy you gain falling the meter or so whle your gear break, these affect the answer by less than 10%.

you fall energy is e =mhg
amount absorbed is z=fd, where f is the force the piece is putting on the rope and d is the distance over which the force is acting. typically f rises from zero up the breaking force.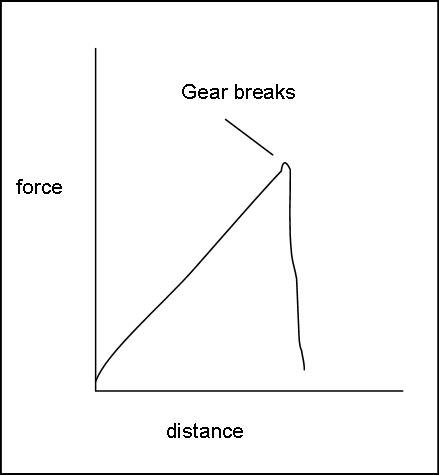

The area under the curve is about z=1/2 fd (the area of the triangle).
Typical values for a fall are
m=80kg
g= 9.8 ms^2
h=5m
so e= 80*9.8*5=3920 J and your speed is v^2=u^2 + 2gh
your velocity v= 9.89m/s

Effect of gear
f=2kn
d=1m
z = 1000J
your new energy is a-e=2920J, which is 74% of what you had before the piece pulled

The decelaration while the gear is pulling is a=g-f/m=-15.2m/s,
which occurs over a time of t=d/v=1m/ 9.89 m/s= 0.101 seconds
you new velocity is v=u+at=9.898+-15.2*0.101 = 8.36 m/s

you velocity has only dropped 16%

if the rope impact force was 4kn and the gear held, e would equal a, the distance the gear loaded you for would be 1.96m


IdratherbeclimbingM9

26-Nov-2009
9:57:10 AM

>a) it's better to have a strategy (equalising, double ropes, slipepry belay) which makes it stay in.

~> I like this better than trying to do maths in my head while on lead!
;-)


Phil Box

26-Nov-2009
8:00:49 PM

Not really the right graph there Mikl. The curve is an exponential increase and then the sudden drop off when the rope or gear breaks. In other words, for the lay people out there, the curve starts reasonably flat and then increases in steepness as it aproaches the breaking point.

This is actually what happens in all the tests graphs that I have been associated with in the real world anyway. There will also be a bump where the gate engages as the biner stretches. facinating to watch actually.

Mike Bee

27-Nov-2009
12:45:15 AM

On 26/11/2009 Phil Box wrote:
>There will also be a bump where
>the gate engages as the biner stretches. facinating to watch actually.

Phil, at what force does this "bump" tend to happen?
I'm curious as to when the the difference between the open and closed gate strength of a carabiner tends to become a factor.


Phil Box

27-Nov-2009
8:17:20 AM

That would depend on the particular brand of carabiner. The steel carabiner that we set up and tested bumped at around 300kgs. I imagine that an alloy screwgate would bump at much less and of course a fairly thin clipgate would engage even lower.

Set up a clip gate in your garage. Hang a rope from a truss or other strong point and tie a loop that you can clip the biner into. Next clip an etrier into the biner and whilst holding the gate side of the biner with your hand wrapped around it put your weight into the biner. You may feel the biner stretch. If not jump up and down on the et.

lacto

27-Nov-2009
8:59:18 AM

On 26/11/2009 Phil Box wrote:
>Not really the right graph there Mikl. The curve is an exponential increase

surely curve is sqare not exponential >

patto

27-Nov-2009
12:23:18 PM

On 26/11/2009 Phil Box wrote:
>Not really the right graph there Mikl. The curve is an exponential increase
>and then the sudden drop off when the rope or gear breaks. In other words,
>for the lay people out there, the curve starts reasonably flat and then
>increases in steepness as it aproaches the breaking point.

His point is still valid though and really it is a common misconception that gear pulling absorbs a meaningful amount energy.

It has been much discussed but I have yet to see any experimental data on this, but theory pretty much says only a negligable quanity of energy is absorbed. As Mikl suggests equalising marginal placements is vital for large falls. Cascading them just leads to cascading failure.

On 26/11/2009 Phil Box wrote:
>This is actually what happens in all the tests graphs that I have been
>associated with in the real world anyway. There will also be a bump where
>the gate engages as the biner stretches. facinating to watch actually.
Thats is cool.

There are 29 messages in this topic.